Data-Structure Vectorization

29 Jul 2021 — Written by Matthias Kretz
Tagged as: AoS, AoVS, C++, SIMD, SoA, and std::simd

One of the major benefits of type-based vectorization is data-structure vectorization. I’ll introduce and hopefully motivate the pattern in this post.

Example and Benchmark

Let me illustrate data-structure vectorization with an example. Consider many points in 3-dimensional euclidean space. We’re given the task to determine the mean distance from the origin (0, 0, 0). A generic definition of a Point is given by

template <typename T>
  struct Point
  {
    T x, y, z;
  };

Now we have at least three sensible choices wrt. vectorization, for storing many points in memory:

// AoS (array of structure)
using Points_AoS = std::vector<Point<float>>;

// SoA (structure of array)
using Points_SoA = Point<std::vector<float>>;

// AoVS (array of vectorized structure)
using Points_AoVS = std::vector<Point<stdx::native_simd<float>>>;

---

A visualization, which I created for my PhD Thesis, might help. It shows how a 4-element structure (a, b, c, d) given 4-element SIMD vectors is located in memory:

• AoS inhibits SIMD loads & stores of a given element from consecutive indexes.
• SoA enables SIMD loads & stores but places the structure’s elements far apart in memory, breaking locality. With the naïve definition above (Point<vector<float>>), the structure elements are even in separately allocated memory, increasing memory allocation overhead.
• AoVS covers the ground in between. It allows SIMD loads & stores while maximizing locality of the structure’s elements.

---

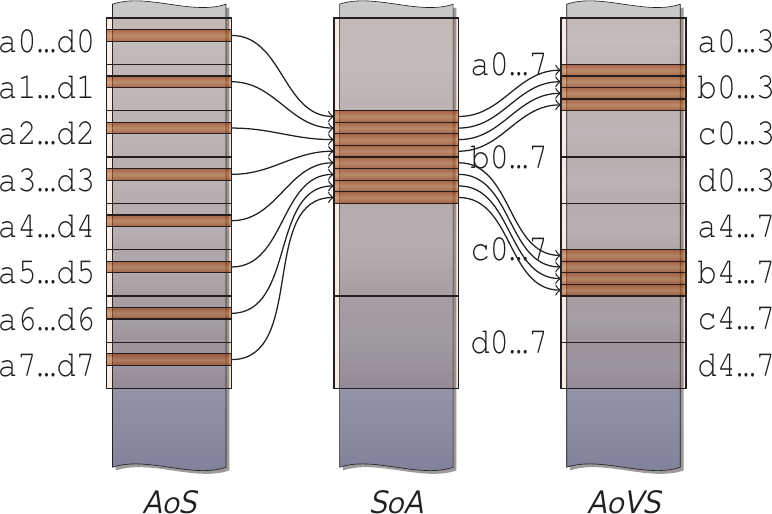
Loop-based vectorization typically uses SoA data layout, because AoS does not perform well. AoVS is often impractical for loop-based vectorization because there is no natural facility for chunking the memory as needed.

Anyway, given these three data structures, we can calculate the mean length by computing the distance to (0, 0, 0) as the root of the sum of squares. After accumulating all lengths, dividing by the number of points yields the mean length:

// AoS ////////////////////////////////////////////////////////////////////////
float mean_length(const Points_AoS& points) {
  float acc = std::transform_reduce(
		std::execution::unseq, points.begin(), points.end(), 0.f,
		std::plus<>(), [](auto p) {
		  return std::sqrt(p.x * p.x + p.y * p.y + p.z * p.z);
		});
  return acc / points.size();
}

// SoA ////////////////////////////////////////////////////////////////////////
float mean_length(const Points_SoA& points) {
  assert(points.x.size() == points.y.size()
           && points.x.size() == points.z.size());
  float acc = 0;
  for (std::size_t i = 0; i < points.x.size(); ++i) {
    acc += std::sqrt(points.x[i] * points.x[i] + points.y[i] * points.y[i]
                       + points.z[i] * points.z[i]);
  }
  return acc / points.x.size();
}

// AoVS ///////////////////////////////////////////////////////////////////////
float mean_length(const Points_AoVS& points) {
  stdx::native_simd<float> acc = 0;
  for (const auto& p : points) {
    acc += sqrt(p.x * p.x + p.y * p.y + p.z * p.z);
  }
  return reduce(acc) / (points.size() * acc.size());
}

The AoVS implementation is straightforward to read, trivially yields SIMD execution, and produces the best results. These are the results on my AMD Ryzen 7 (AVX for native_simd<float>) with GCC 11.2, compiled with -O3 -march=native:

                  TYPE        fast-math   mean_length
                                        [cycles/call] (smaller is better)
-----------------------------------------------------------------------------
 float                    SoA        no  9800 ██████████████████████████████
 float                    AoS        no  9695 █████████████████████████████▋
 float                    AoS       yes  4404 █████████████▌                
 float                    SoA       yes  1541 ████▊                         
 float, simd_abi::[AVX]   AoVS      yes  1238 ███▊                          
 float, simd_abi::[AVX]   AoVS       no  1230 ███▊                          
-----------------------------------------------------------------------------

As you can see, -ffast-math (and also -O3, -O2 typically suffices for stdₓ::simd) is necessary for good SoA performance. Independent of -ffast-math and -O2 vs. -O3, AoVS with stdₓ::native_simd<float> wins. SoA performance with auto-vectorization is close, but AoS performance is always bad.

Patterns

The Point template as defined above is a typical pattern I like to use. You can even give it member functions which depend on T. For example we can add a distance_to_origin() function to Point:

template <typename T>
  struct Point
  {
    T x, y, z;

    T distance_to_origin() const {
      using std::sqrt;
      return sqrt(x * x + y * y + z * z);
    }
  };

Then, if you’re careful about if statements, you can instantiate the template with either an arithmetic type or a stdₓ::simd type. You’ve effectively declared a template that is vectorizable in terms of data layout and algorithms.

Objects of Point<simd> are the working sets the program subsequently would use whenever possible. Thus, you may see these vectorized user-defined types cross function boundaries. They become an integral part of your internal APIs.

ABI concerns

If you require a stable ABI at a library boundary, then you need to understand how it affects your ABI. The use of stdx::native_simd explicitly asks for an ABI dependency on compiler flags. The stdx::simd_abi::fixed_size<N> ABI tag was specifically implemented in libstdc++ such that it trades performance for ABI stability. The use of stdx::fixed_size_simd<T, N> on ABI boundaries can be considered safe and stable.